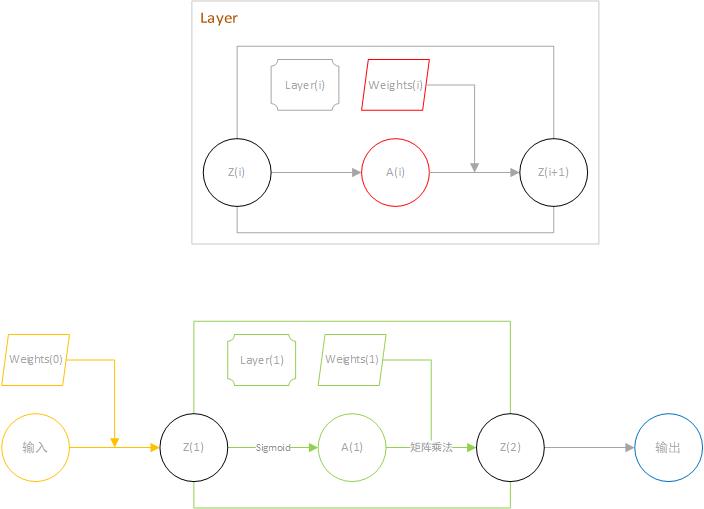
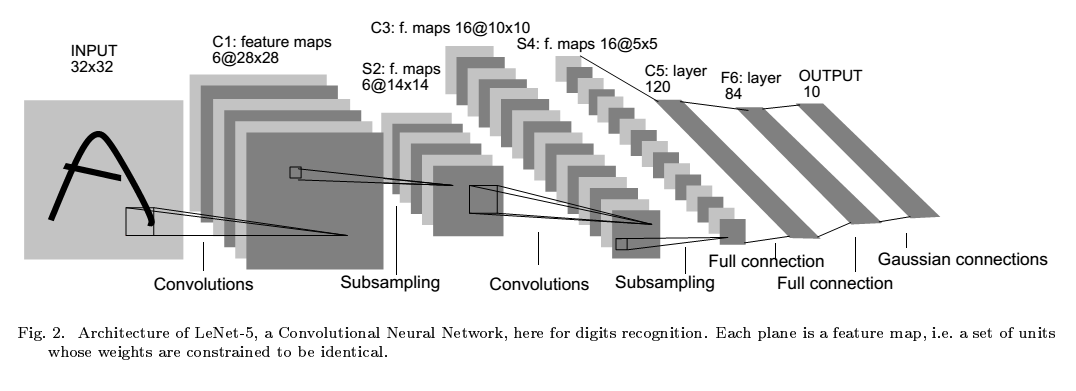
lenet5 实现了手写数字的识别。其关键在于CNN的使用。其结构如下:
convolution
通俗地理解卷积运算 数学表达式:
$$ (fg)(x) = \int_{-\infty}^\infty f(\tau)g(x-\tau)d\tau $$
可以把$f(x)$理解为信号,$g(x)$理解为发出信号的时机。那么卷积就代表了当前时刻该信号的叠加效果。在图像中卷积的意义。虽然卷积的过程看上去很像内积,但其实两者有很大的区别,两者的前进方向不同。为了方便计算,将g中的下标进行修改,使得卷积运算可以直接用内积来表示。(将g旋转$180\degree$)
卷积后得到的矩阵称为feature map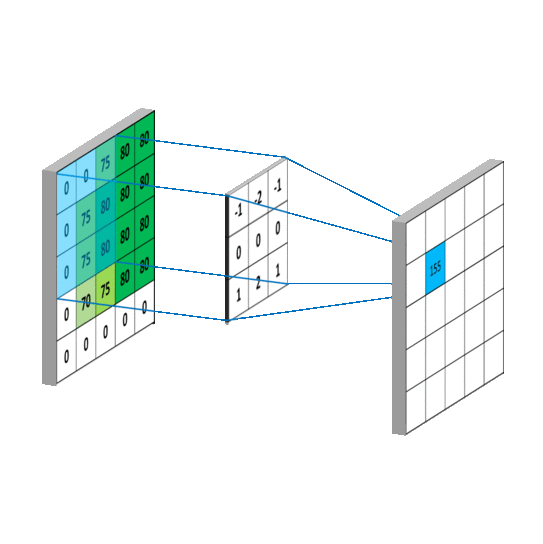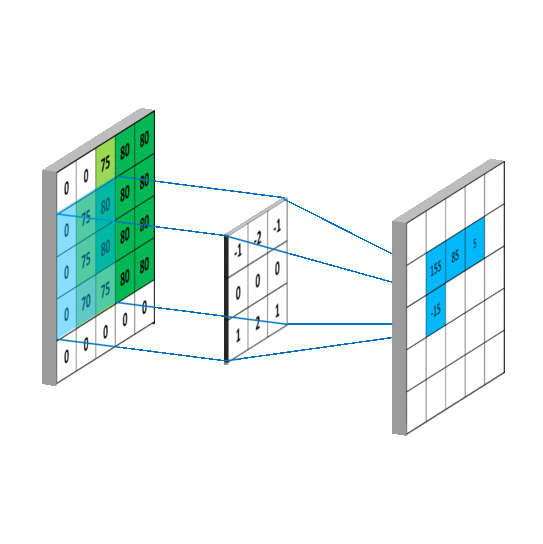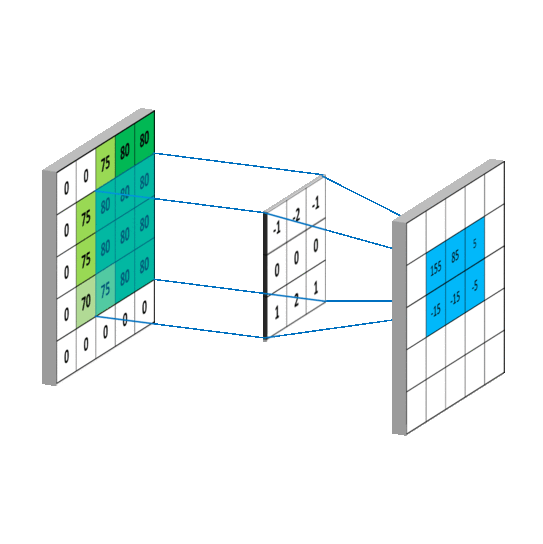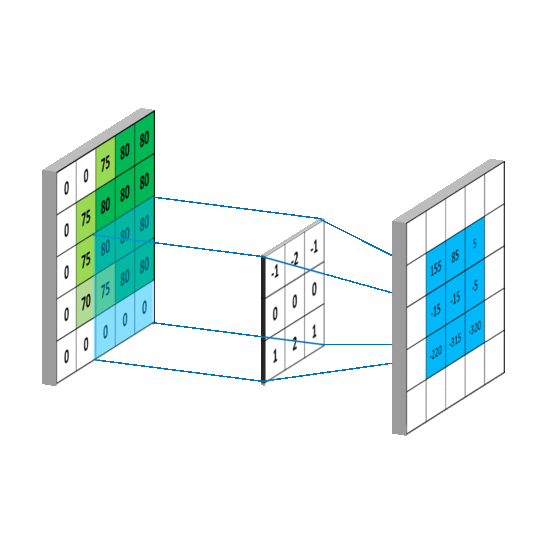
如果特征刚好在角落上,那么上面的卷积过程无法检测到。因此,可以在输入矩阵上填充padding。同时使得输入与输出的大小相同。 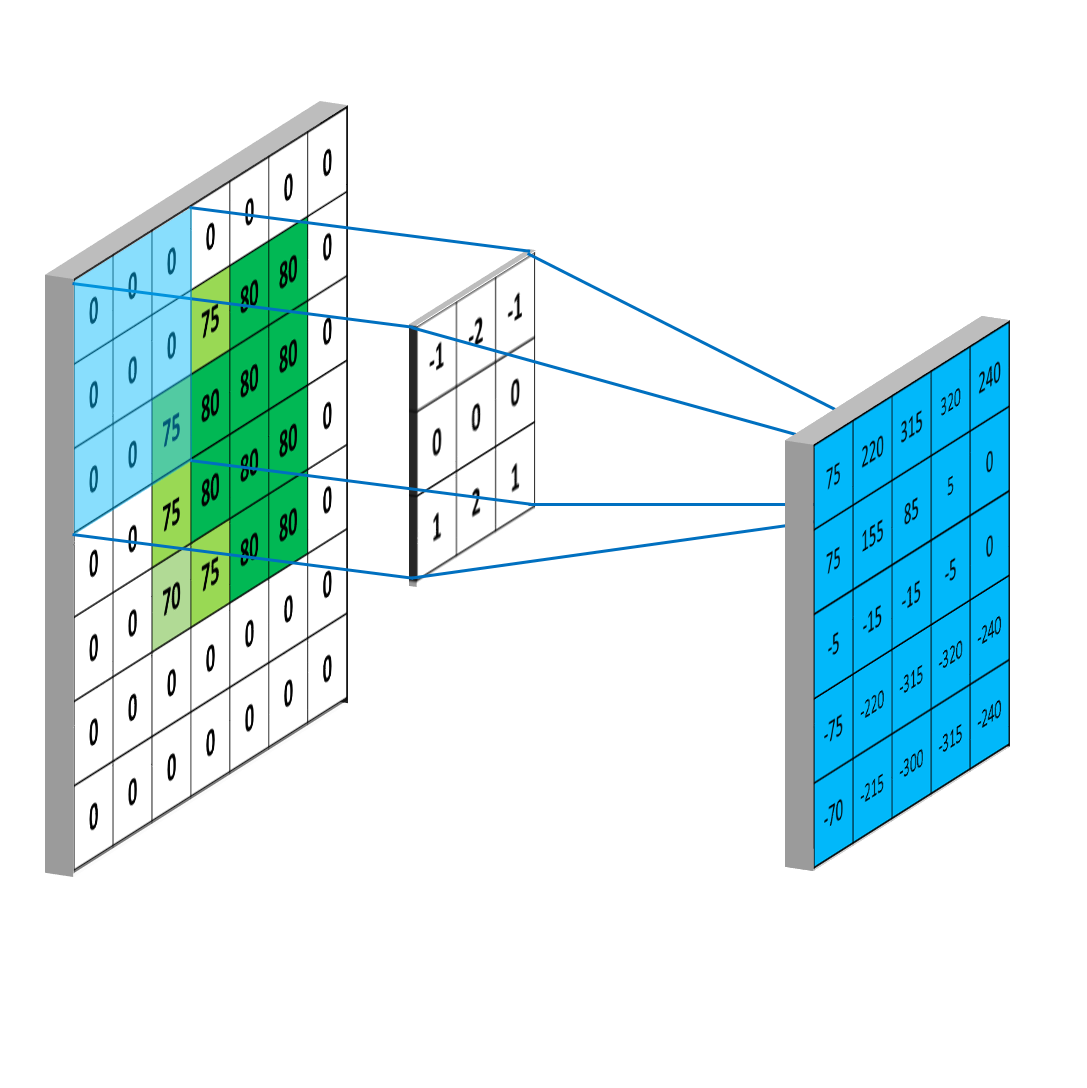
也可以控制stride来改变卷积核的移动步伐.这会导致feature map的尺寸变小。
设输入的尺寸为 $I_r \times I_c$ , 卷积核尺寸为$K_r \times K_c$, 则可训练参数为$K_rK_c+1$,输出尺寸为$(I_r+1-K_r) \times (I_c+1-K_c)$.(无padding,stride=1)
Convolutional Layer
作为神经网络,每一个节点只有2种状态(激活或者未激活)。在感知机中使用sigmoid函数进行激活使得输出值在[0,1]。这一过程被称为Non-linearity。
Pooling Layer
这一过程比较简单,它将原图像进行分割。再对每一个区域进行一次计算。与卷积不同的是,这里的每一块区域都是不重叠的。最终它使得输入尺寸成倍地减少。这一操作称为subsampling 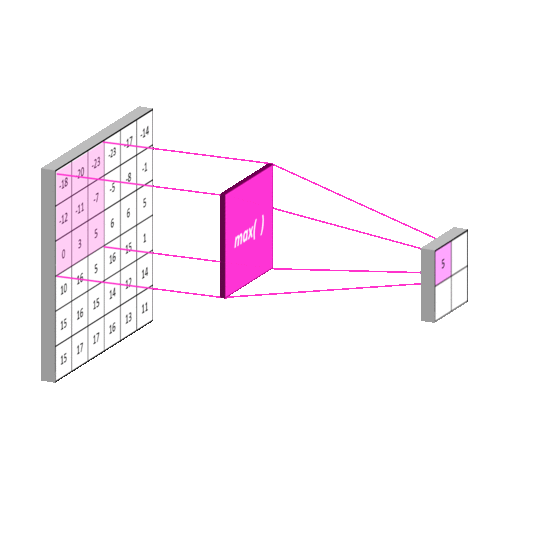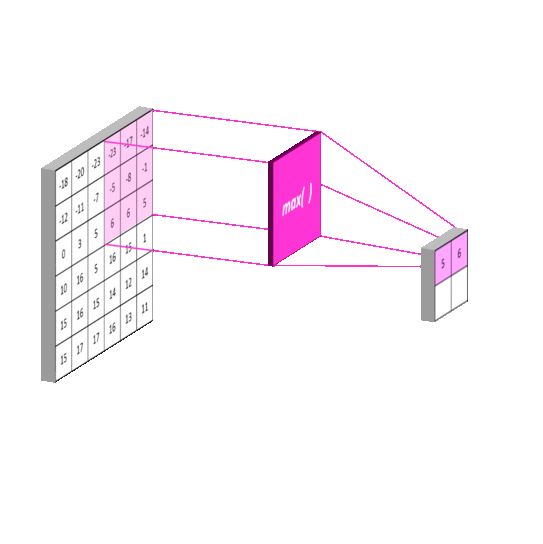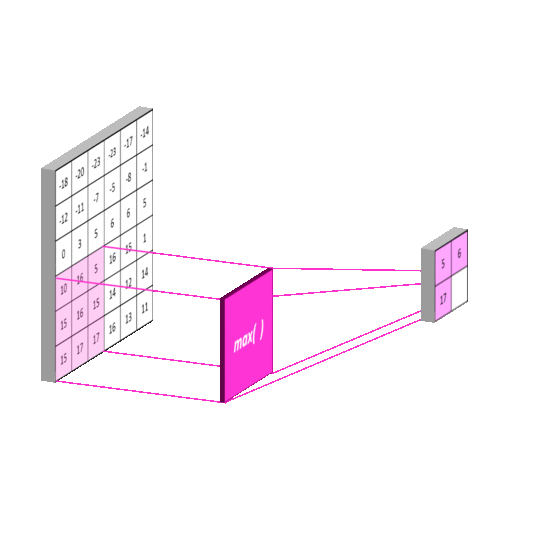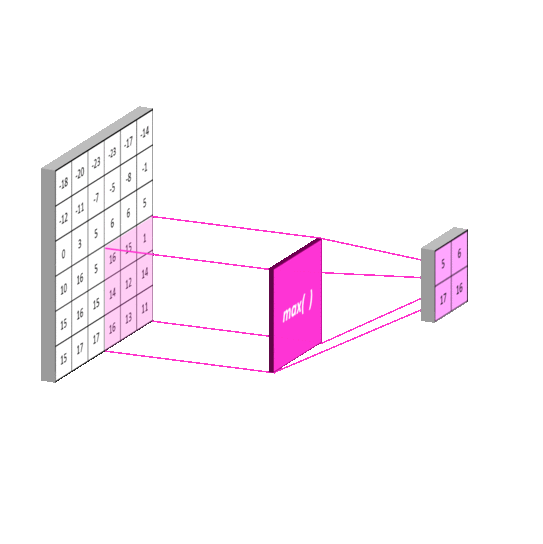
每一层含有2个参数,coefficient and bias。同样,作为神经网络中的一层,需要对subsampling后的数乘以coefficient+bias 再用sigmoid函数激活才能输出到网络中。
Fully-connected (Dense) Layer
这一层与多层神经网络相同,不同的是它的输入可能具有多个channel。不管怎么样,都可以将输入看作是一维的。
Practice
这里我遵照lenet5原始论文进行复现。材料:数据集+论文
预处理
背景色置为-0.1,前景色为1.175. (raw-20)/200
C1
这里有点奇怪,论文里说输入图像是32X32的,但是数据集是28X28的。
6个 zero-padding5X5的卷积层。有$655+6(bias)=156$个参数。$62828=4704$个神经元。
输出:$6\times28\times28$
S2
大小为:2X2.取区域平均值×系数+bias再sigmoid激活。 参数:$6\times 2$
输出:$6\times14\times14$
C3
这里卡了很久,不知道多个feature map 如何进行卷积。其实可以把多个feature map当作多个通道,每个通道上各自进行卷积再叠加在一起。或者说这个卷积具有3维结构(前面都是二维的),只不过其中一维的大小为3,因此正好被压回2维结构。3X14X14的输入,3X5X5的核。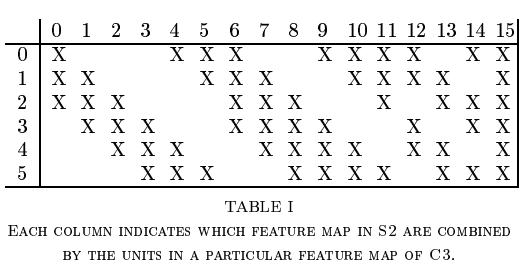
参数:3X5X5 6个,4X5X5 6+3个,6X5X5 1个
输出:16X10X10
S4
大小为:2X2.取区域平均值×系数+bias再sigmoid激活。
输出:$16\times5\times5$
C5
大小为:16X5X5. 共120个。
输出:120X1
F6
使用正切函数激活。
$$ f(a)=A tanh(S*a) $$
A为1.7159.
输出:84
output
计算公式:
$$ y_i=\sum_j(x_j-w_{ij})^2 $$
如果模型有k个输出,即k个分类。那么$w_{k*}$代表了该类别在特征空间中的位置。显然,离该特征向量越远,输出越大。这称为distributed code
Loss function
关键代码
写了一通代码发现直接炸了,运算速度实在太慢,简直出不了结果。实验了一下发现python的for循环效率极低,要实现神经网络,必须全部使用专门优化过的工具。如numpy,最好全程使用矩阵运算并避免矩阵的复制。使用卷积的时候可以利用im2col1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46def use_time(f,c=1,*args):
import datetime
start = datetime.datetime.now()
for i in range(c):
f(*args)
return datetime.datetime.now()-start
def im2col(image, ksize, stride):
# 100 , 5,1 0:00:12.587087
# image is a 4d tensor([batchsize, width ,height, channel])
image_col = []
for i in range(0, image.shape[1] - ksize + 1, stride):
for j in range(0, image.shape[2] - ksize + 1, stride):
col = image[:, i:i + ksize, j:j + ksize, :].reshape([-1])
image_col.append(col)
image_col = np.array(image_col)
return image_col
def im2col1(image, ksize, stride):
# 0:00:02
shape_r =(image.shape[0] - ksize + 1)//stride
shape_c =(image.shape[1] - ksize + 1)//stride
channel=image.shape[3]
m = image.shape[0]
col = np.zeros([shape_r*shape_c,ksize*ksize*channel*m])
for i in range(shape_r):
for j in range(shape_c):
col[shape_r*i+j,:] = image[:, i:i + ksize, j:j + ksize, :].reshape([-1])
return col
def im2col2(image, ksize, stride):
# 100 , 5,1 0:00:12.587087
# image is a 4d tensor([batchsize, width ,height, channel])
image_col = []
for i in range(0, image.shape[1] - ksize + 1, stride):
for j in range(0, image.shape[2] - ksize + 1, stride):
col = image[:, i:i + ksize, j:j + ksize, :].reshape([-1])
image_col.append(col)
return np.concatenate(image_col)
images=np.random.rand(10,100,100,6)
print(use_time(im2col,100,images,5,1))
print(use_time(im2col1,100,images,5,1))
print(use_time(im2col2,100,images,5,1))
Appendix
implement
sigmoid
wiki
它是一类具有形如”S”的函数。常指Logistic function
BP
Pooling池化操作的反向梯度传播
在计算卷积的偏导数时,可以先把不同单元的权值当作是不同的分开计算,最后再把他们加起来。这就好比分身术,先产生n个分身,然后分身再合体回一个。它其实就是一个全微分:
$$ df(x_1,x_2)=f’{x1} d{x1}+f’{x2}d{x2} $$
如果令$x_1=x_2=x$就得到了上面的方法。