概述

Hopfield Network 最大的特点是所有神经元都在同一层,而且是全连接的.通常来讲，带有循环连接和非线性神经元的网络不太好分析，因为其行为比较难以捉摸：它们可以陷入稳态，可以振荡，甚至可以陷入混沌(除非你知道无限精度的初始状态，否则无法预测不远的将来的状态).所以Hopfield Network做出了一点限制,连接矩阵$W_{ij}$要求对称,$W_{ii}=0$.

效果

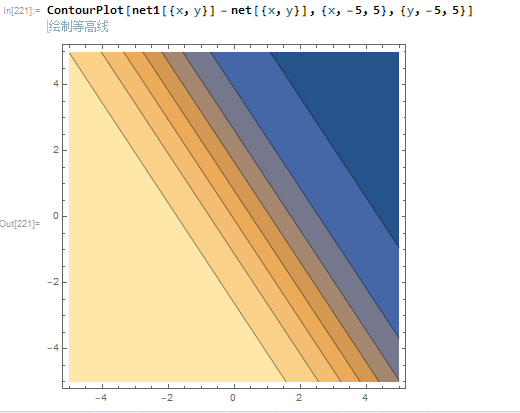
能够存储信息,起到联想记忆的效果.

第一行为训练的图片,第二行是加入噪声的图片,第三行是使用Hotfield Network还原后的图片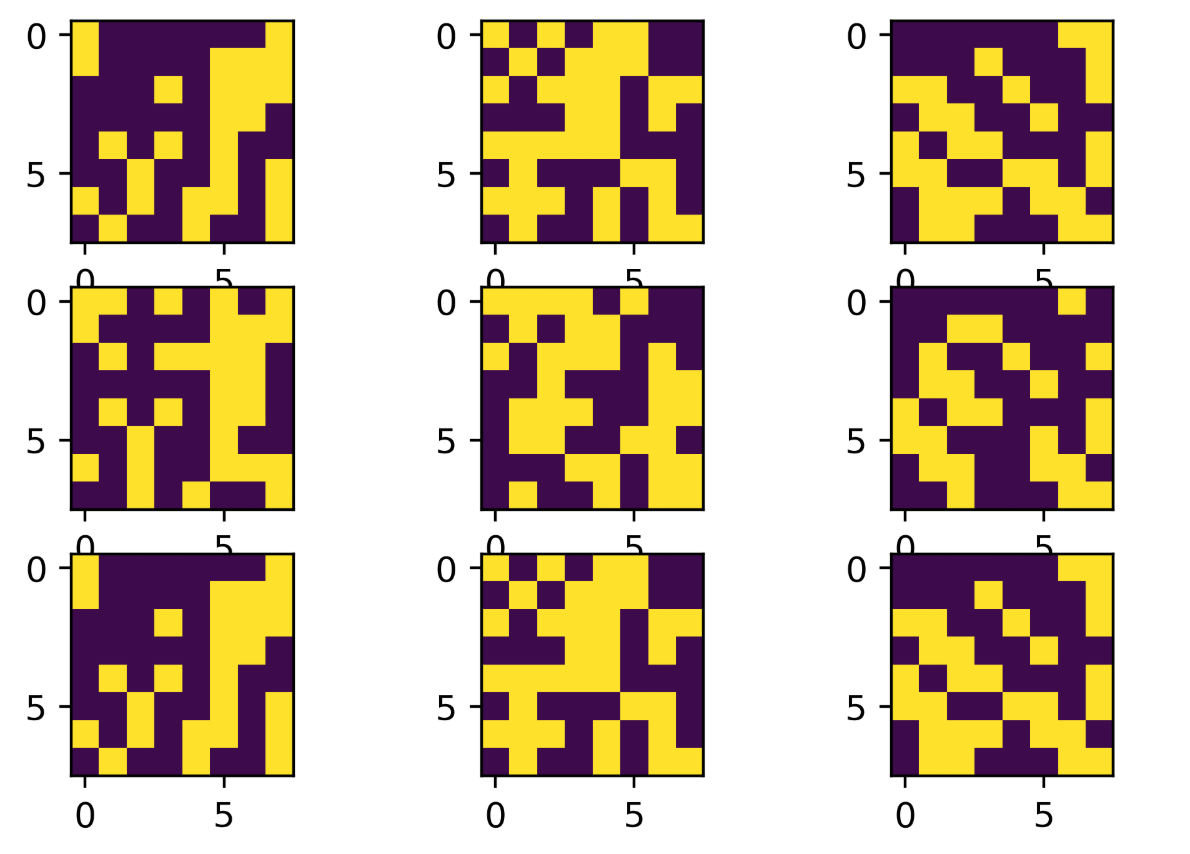

Reference

Artificial Neural Network - Hopfield Networks

Hopfield神经网络

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

def E(W,V,input):
    n=len(input)
    e=0
    for i in range(n):
        for j in range(i):
            e+= -W[i,j]*V[i]*V[j]
    for i in range(n):
        e+=-input[i]*V[i]
    return e
def train(sample_set):
    m,n=sample_set.shape
    W = np.zeros((n,n),dtype=int)
    for i in range(n):
        for j in range(n):
            if i == j:
                continue
            W[i,j]=((2*sample_set[:,i]-1)*(2*sample_set[:,j]-1)).sum()
    return W
def test(sample,W):
    V = sample.reshape(-1).copy()
    l = len(V)
    e=0
    e1=1
    while e!=e1:
        for i in np.random.choice(range(l),l,False):
            V[i]+=V.dot(W[:,i])
            if V[i]<0:
                V[i]=0
            if V[i]>0:
                V[i]=1
        e1=e
        e=E(W,V,sample.reshape(-1))
        print(e)
    return V.reshape(sample.shape)

sample = np.random.randint(2,size=(3,8,8),dtype=int)
W=train(sample.reshape(3,-1))
fig,axes =plt.subplots(3,3,dpi=200)
for i in range(3):
    axes[0,i].imshow(sample[i])
    t = sample[i].copy()
    mask =np.random.rand(8,8)<0.2
    t[mask]=1-t[mask]
    axes[1,i].imshow(t)
    axes[2,i].imshow(test(t,W))

Momory and Attractor Dynamics

Hopfield Model

Hopfield model包含$N$个神经元.在Hopfield model中每个神经元只有两个状态$S_i$.(一般有二种表示方式,0/1或者-1/1).以离散的时间步长$\Delta t$动态地演化.
神经元之间通过$w_{ij}$相互作用.某一神经元的输入对其他神经元的影响可以表示为:
$$h_{i}(t)=\sum_{j}w_{ij}\,S_{j}(t)\,.$$
在t时刻输入(The input potential)影响下一时刻状态变量$S_i$的更新概率:
$${\rm Prob}{S_{i}(t+\Delta t)=+1|h_{i}(t)}=g(h_{i}(t))=g\left(\sum_{j}w_{ij}%
\,S_{j}(t)\right)\,$$
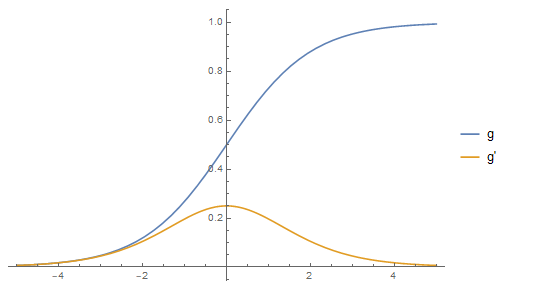
这里g是一个值域为0-1且单调递增的增益函数(gain function).一般选择使用$g(h)=0.5[1+\tanh(\beta h)]$.如果$\beta\to\infty$,那么当$h>0$时$g(h)=1$否则为0.其动力学由此确定并且总结出更新规则(The dynamics are therefore deterministic and summarized by the update rule)
$$S_{i}(t+\Delta t)=\operatorname{sgn}[h(t)]$$
因为无限大的$\belta$是随机的.下面我们假定每一步更新神经元都是同步的(一起更新),但是另一个可能的更新方案是一次只更新一个神经元.

这一节的目的是说明选择合适的耦合矩阵(coupling matrix)$w_{ij}$可以记忆内容.

Detour: Magnetic analogy

磁性材料含有携带指针(a so-called spin)的原子.这个指针在微观下产生磁矩( magnetic moment),如图17.5A所示.在高温下磁矩可能指向任何方向.在低于一定温度下,所有原子的磁矩自发地互相对齐.结果所有原子磁矩的微观效果叠加使得材料出现磁性.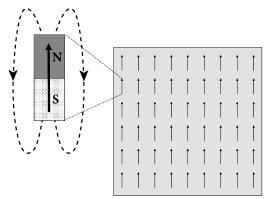

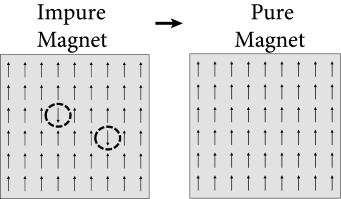
为了理解自发对齐是如何产生的,我们通过研究等式(17.2)(17.3)来类比磁性材料.我们先假定$w_{ij}=w_{0}>0$,$i!=j$,$w_{ii}=0$.

每一个原子被赋予一个变量$S_{i}=\pm 1$,+1表示向上,-1表示向下.在$t=0$的时候,所有指针取+1,除了部分原子$S_{i}(0)=-1$.我们可以计算在$t=\delta t$时神经元i切换到$S_i=+1$的概率:
$${\rm Prob}{S_{i}(t+\Delta t)=+1|h_{i}(t)}=g(h_{i}(t))=g\left(\sum_{j=1}^{N}w_{ij}\,S_{j}(t)\right)=g(w_{0}\,(N-1))$$
这里$g(h)=0.5[1+\tanh(\beta h)]$,$w_{0}=\beta=1$.在物理系统中,$\belta$起到逆转温度的作用.如果$\belta$太小(高温),磁矩不再对齐并且材料失去自发组织的性质.

通过上式发现网络的规模越大概率也越大.我们的这个人工模型是在所有的原子直接相互作用.而在物理世界中,作用力随着距离增大快速地下降.所以式子可以改写成最近的4到20个邻居.但是有趣的是,神经元不同与原子,可以产生大范围的作用.因为他们有轴突(axonal cables )和树突(dendritic trees).因此神经元的拓扑邻居( topological neighbors)的数目是上千.

一个完美对齐排列的磁场看起来很无聊,但是物理学上有一些有趣的例子.在一些材料中,有2类不同的原子A和B,比如抗磁铁(anti-ferromagnets).如17.6A所示一个向上另一个向下,总和为0.

为抗磁铁做一个模型,我们选择作用力$w_{ij}=+1$如果i和j是用一种类别,否则为-1.利用算式(17.5),显示出在低温下抗磁铁的磁矩的组织方式.

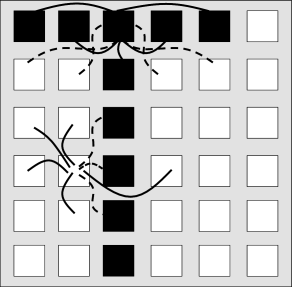
同样的思路可以用在神经网络中,使用正负值表示相互作用力.图17.6B显示了神经元的激活(+1)和抑制(0-1).从抗磁铁提取出的规则意味着不同颜色神经元所连接的权值是负的,相同颜色为正.
$$w_{ij}=p_{i}\,p_{j}\,.$$
这个公式是Hopfield model的基础.

Hopfield 模型中的模式

Hopfield模型包含N个神经元,能够存储M个不同的模式. 模式$u, 1\leq\mu\leq M$.每一个模式被定义为一组期望配置(desire configuration)$\left{p_{i}^{\mu}=\pm 1;1\leq i\leq N\right}$.网络中的N个神经元能纠正模式u,如果$S_{i}(t)=S_{i}(t+\Delta t)=p_{i}^{\mu}$.

在网络的建立阶段,一个随机数值生成器生成为每个模式u的字符串.该字符串有N个独立的数字${p_{i}^{\mu}=\pm 1;1\leq i\leq N}$,带有明确的值$\langle p_{i}^{\mu}\rangle=0$.不同模式见的字符串是独立的.权值通过下式选择:
$$w_{ij}=c\sum_{\mu=1}^{M}p_{i}^{\mu}\,p_{j}^{\mu}\,$$
其中$c>0$.网络是全连接的.如果是单模式且$c=1$,那么该式子就和抗磁铁一样.一般选择$c=1/N$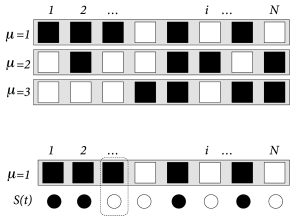

Fig. 17.7: Hopfield model. A. Top: Three random patterns μ=1,2,3 in a network of N=8 neurons. Black squares (pμi=+1) and white squares (pμi=−1) are arranged in random order. Bottom: The overlap m1=(1/N)∑ip1iSi(t) measures the similarity between the current state S(t)={Si(t);1≤i≤N} and the first pattern. Here only a single neuron exhibits a mismatch (dotted line). The desired value in the pattern is shown as black and white squares, while the current state is indicated as black and white circles; schematic figure. B. Orthogonal patterns have a mutual overlap of zero so that correlations are Cμν=(1/N)∑ipμipνi=δμν (top) whereas random patterns exhibit a small residual overlap for μ≠ν (bottom).

模式恢复

在很多记忆恢复的实验中,在回忆事件开始时给出局部信息的线索.通过验证丢失信息的完成度来评估记忆内容的恢复程度.

为了在hopfield 模型中模仿记忆恢复,给出网络初始值$S(t_{0})={S_{i}(t_{0});1\leq i\leq N}$.初始化后,网络在动力学下自由演化.理想情况下动力学会收敛到一个固定的相关模式u上,这个模式与初始状态是最接近的.

为了衡量相似度,我们提出重叠.(每个点相同为1不同为-1)
$$m^{\mu}(t)={1\over N}\sum_{i}p_{i}^{\mu}\,S_{i}(t)\,.$$
如果模式被恢复重叠度最大为1,当$S_{i}(t)=p_{i}^{\mu}$.如果当前状态与模式u完全不相关,它会接近于0.如果每个神经元的取值都相反,此时达到最小值$m^{\mu}(t)=-1$.

重叠度在分析网络动力学中扮演了重要作用.实际上,输入$h_i$是:
$$h_{i}(t)=\sum_{j}w_{ij}\,S_{j}(t)=c\sum_{j=1}^{N}\sum_{\mu=1}^{M}p_{i}^{\mu}\,%
p_{j}^{\mu}\,S_{j}(t)=c\,N\,\sum_{\mu=1}^{M}p_{i}^{\mu}\,m^{\mu}(t)$$
为了使结果无关于输入规模的大小,使用标准化系数$c=1/N$.下面除非特别说明,总使用这个系数.

为了进一步讨论,我们现在在动力学公式并且发现
$${\rm Prob}{S_{i}(t+\Delta t)=+1|h_{i}(t)}=g\left[\sum_{\mu=1}^{M}p_{i}^{\mu}%
\,m^{\mu}(t)\right]\,.$$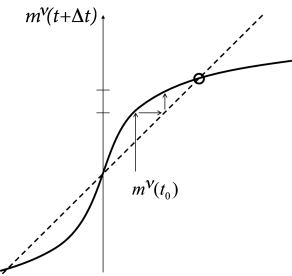

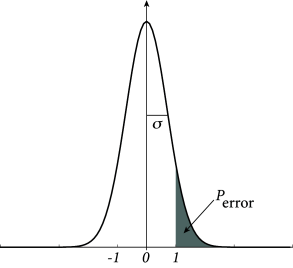
Fig. 17.8: Memory retrieval in the Hopfield model. A. The overlap mν(t+Δt) with a specific pattern ν is given as a function of the overlap with the same pattern mν(t) in the previous time step (solid line); cf. Eq. (17.16). The overlap with the M−1 other patterns is supposed to vanish. The iterative update can be visualized as a path (arrow) between the overlap curve and the diagonal (dashed line). The dynamics approach a fixed point (circle) with high overlap corresponding to the retrieval of the pattern. B. The probability Perror that during retrieval an erroneous state-flip occurs corresponds to the shaded area under the curve; cf. Eq. (17.20). The width σ of the curve is proportional to the pattern load M/N; schematic figure.

神经元计算公式为:
$$a=g(w_i^T x)$$
g为sigmoid函数,其特点是在左侧接近0,在右侧接近1,其导数也具备类似性质.

再看BP算法中梯度的计算.

$$\delta^l=\frac{∂z^{l+1}}{∂z^{l}}=w^{k^T}z^{l+1}.*a^l.∗ (1−a^l)$$
$$\frac{∂J}{∂w^{l}}=\delta^{l+1}a^{l^T}$$

与第l层神经元$a^l$有关的权值有$w^{l}$,$w^{l+1}$.$a^l$越大,$w^{l+1}$的梯度越大;而$a^l$太大或者太小,$w^{l}$的梯度都越小.总的来说就是$a^l$接近0,那么对前后的权值都没有影响.如果接近0.5,那么前后的权值都能得到调整.如果接近1,那么只有后面的权值能够得到调整.

前后weight

前部weight决定了该神经元是否被激活,而后部weight决定了最后输出的形状.用$w_1$,$w_2$表示.
如果神经元的值为0或者1,那么它不能产生有效的形状,因此是无效的.
$$-4<w_1 x+b<4$$
$$w_1 x+b=0$$
所以神经元的有效区间长度为$8/w_1$,区间为$[(-b-4)/w_1,(-b+4)/w_1]$

这样就可以对神经元进行可视化.实际上最后的曲线是多个神经元叠加的效果,而这里显示的是单个神经元的效果.

$$ len=8/w, center = -b/w$$

调整神经元形状

$$ len = -8center/b$$
这个算式说明,中心远离原点的神经元其有效区间长度也比较大.也就是说在远处神经元无法精确拟合一段函数.
对原来的算式进行一点修改,
$$a=g(k(w_i^T x))$$
得到:
$$ len=\frac{8}{k*w}, center = -b/w$$
这样就在不改变中心点位置的情况下调整有效区间的长度,因而可以提高神经网络的精细程度.

如图为k=0.3时的图形,此时函数可以看作是多个神经元叠加的效果,因此更加光滑.

因此如果神经元数量过多,而数据量太少就会导致的过拟合.其实就是部分神经元没有得到训练,因为他们的有效区间很窄.通过正则化,减少权值大小,扩大有效区域长度.但是如果神经元的有效区域太大,最后的形状就是所有神经元共同决定的,这样也就很难习得精确的形状.

60个神经元拟合sin函数,k=1

那么反过来,提高weight减少有效区长度.这样保证在一段内只有少数神经元得到激活训练,这样可以获得更加精确地拟合.

60个神经元拟合sin函数,k=10

总结

这也解释了神经网络中的很多事

为什么要对数据进行处理?

由于目前神经网络初始化的方法导致神经元的中间往往在原点附近,因此远离原点的数据收敛也慢.

为什么深度网络难以训练?

除了梯度爆炸\梯度消失等问题外,由于每增加一层网络都会产生一些没有被激活或者是饱和的神经元,到最后一层时,有效区域变得很少.

二维数据的理解

同样对于一层神经元可以分为前后两部分,前部的weight和bias选择区域,后部的weight和bias决定形状.我选择一个二元函数来验证这一点:
$$z=\sin \left(x+0.1 y^2\right)$$

使用20个隐层神经元的网络来拟合该函数.

利用公式
$$ -3<xw_1+ y w_2 + b<3$$
得到有效区域.

然后分别将第8,10个神经元的后部权值置0(抹除该神经元的效果)后与原输出相减,绘制等高图.


蓝色为0,黄色越深数值越大.

#总结
因此神经网络可以理解为选择与重构.一个神经元选择数据集中的部分区域得以激活,然后在这块区域重构出目标函数的形状.

家里的电视盒升级了,过来的安装的时候发现除了一个机顶盒还有一个解调器.那么问题来了,能否白嫖广电的网络呢?

研究方法

首先尝试直接将猫连接到路由器的WLAN口上,发现无法取得IP.那么有两种可能,1.需要拨号;2.只能访问特定的IP(广电的内部网络).取一个路由器,将猫与机顶盒都接在路由器的lan口上,这样路由器就起到了hub的效果,所有机顶盒访问的数据可以在lan上广播.再将PC连接无线到路由器上,用wiresharp抓包.

抓包

非常不幸的是无法获取到机顶盒发出的报文信息,但是确实需要网线才能播放节目,拔出网线后,节目无法播放.难道还有wiresharp不能捕获的数据包?

访问

既然不知道机顶盒是如何通信的,那只能看看目前的网络是一个怎样的结构.

在dns服务器同一网段下有不少设备,在浏览器中输入IP地址可以看到华为的landswitch登陆界面.还有的是zDNS.上图是tracert其中一个ip后,得到的一个中间节点.也就是机顶盒与DNS服务之间的一层的设备.

结论

这个广电的猫确实能够访问外网,但是这个网络应该是一个大型的城域网,或者只能在广电内部访问.因此想白嫖是不可能的了.似乎能够使用IPTV,在电脑上播放电视.但是没啥用,不整了~~