定义:

一棵空二叉树是AVL树，如果T是非空二叉树，TL和TR分别是其左子树和右子树，
则当且仅当TL和TR都为AVL树且|HL-HR|<=1时，T是AVL树。
AVL树的高度:（固定节点数计算最大高度）
AVL树节点的平衡因子:
AVL树节点的平衡因子定义为其左子树的高度减去右子树的高度，我们可以在插入和删除操作的时候更新平衡因子。
一棵AVL树的各节点平衡因子为1，-1, 0

树的旋转:

当树的平衡因子的绝对值大于1，则该avl树不平衡。旋转通过调整子树和根的位置来重新获得平衡。

理论分析:

T代表树根节点，TL代表左子树，TR代表又子树。以此类推。*H表示树高。’代表旋转后的新值。

由于旋转具有对称性，所有只讨论左旋。

左旋后以TR的节点为根(T’=TR)，TRR成为新的右子树(TR’=TRR)。TL’=T

HL’=max(HL,HRL)+1。

新的平衡因子G’为HL’-HR’=max(HL,HRL)-HRR+1;

HL-max(HRL,HRR)-1<-1 => HL< max(HRL,HRR)

若HRL>HRR,HL,G’=GR’+1.有可能破坏平衡

若HRR>HRL。HL<HRL,G’=GR’+1(不会破坏平衡)

针对HRL>HRR,使用特殊的旋转。

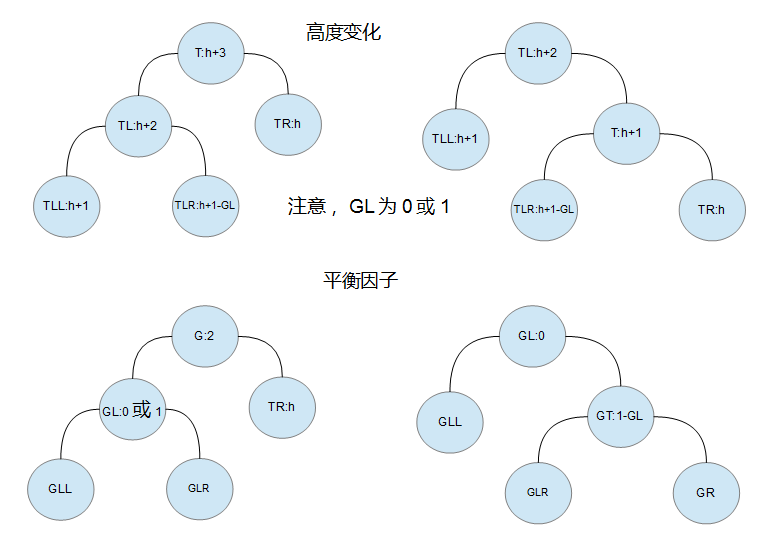
实际分析:

G代表平衡因子。
插入操作，导致某处的G为2或-2.
右旋时的分析:

针对GL==-1这种情况简单右旋不能使之平衡。故使用左-右旋。

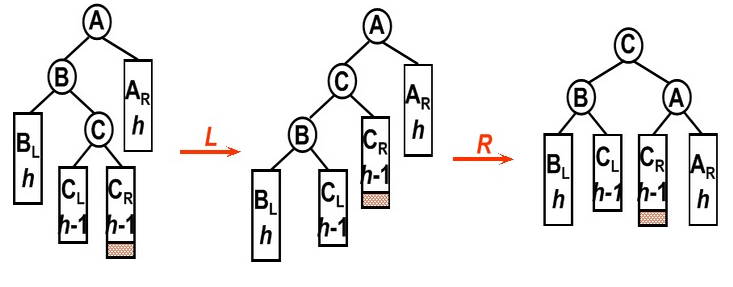
对于左旋，有相同的性质，只是左右互换。
由此推出以下性质:

1. 旋转不会改变其子树的平衡状态
2. 旋转以后会使树高-1.

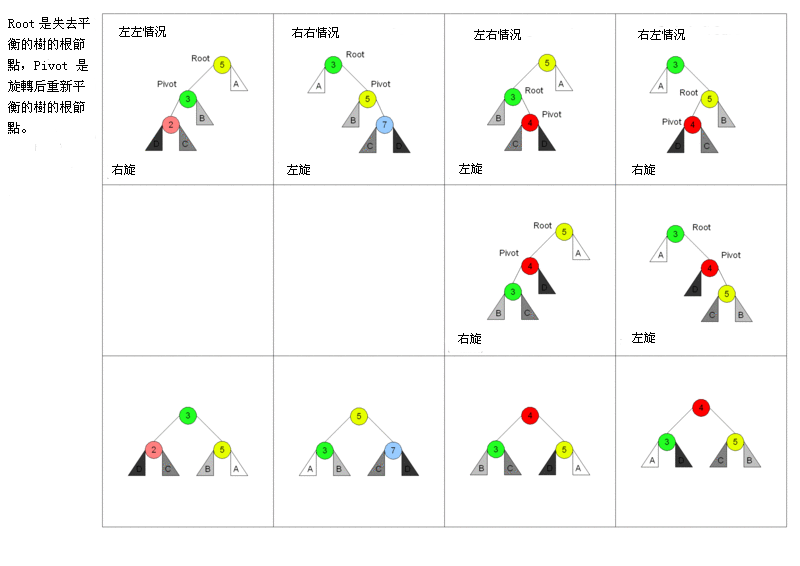
插入:随着插入，树的平衡性会被打破，此时可以4种选择方法解决。

1. 简单右旋:当插入项位于最近的平衡因子为+2的祖先节点的左孩子的左子树中时。LL
2. 简单左旋:当插入项位于最近的平衡因子为- 2的祖先节点的右孩子的右子树中时。RR
3. 左—右旋:当插入项位于最近的平衡因子为+2的祖先节点的左孩子的右子树中时。LR
4. 右—左旋:当插入项位于最近的平衡因子为- 2的祖先节点的右孩子的左子树中时。RL
   这样旋转以后树的高度不变。

D为插入的元素。

插入操作
旋转操作能使树高-1，使破坏的平衡恢复
当G=-2时，使用左旋，G’=GR+1。 仅当GR=-1时GL’=0，其余GL’=-1.
若GR=1,则对TR使用右旋，GR’=-1,再对T使用左旋，G’=0.
当G= 2时，使用右旋， G’=GL-1。仅当GL= 1时GR’=0，其余GR’=1.
若GL=-1,则对TL使用左旋， GL’= 1,再对T使用右旋，G’=0.

插入时使用递归函数可以获得子数的状态，通过返回一个高度参数grow，来进行平衡因子的修正。

1.根据数值判断插入的方向
int g;
if(insertData(pNode->m_pLChild,data,g,route)==exist)
2.若左子树增长，在G==-1时，树高不变。在其余情况下树高增加。
若右子树增长，在G== 1时，树高不变。在其余情况下树高增加。
3.判断是否破坏平衡。

删除操作

1
2
3

删除元素有可能使树高-1，使用平衡操作（旋转）后。该子树进入平衡状态，但有可能导致父节点的不平衡。
类似插入操作，通过递归来获得树高的变化。
但是在子树高度减少的情况下树高变化不同。

若左子树减少，在G== 1时，树高不变。在其余情况下树高减少。
若右子树减少，在G==-1时，树高不变。在其余情况下树高减少。

以上分析对删除叶节点有效，在删除中间节点时。删除节点的子树处理比较困难。
因而使用交换，将删除节点与右子树的最小元素交换。再使用删除操作，转化为删除叶节点。

程序分析:
对T的右旋操作

1.将保存L,断开T-L,。

2.断开L-LR,LR成为T的左子树

3.T成为L的右子树，L成为新的根。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

int balance(avl* &root,int cl,int cr)
{
	avl*tl=root->l,*tr=root->r;
	avl* t=root;
	if((cr-cl)==2){
		if(deep(tr->l)>deep(tr->r)){
			auto nroot=tr->l;
			t->r=nroot->l;
			tr->l=nroot->r;
			root=nroot;
			root->l=t;
			root->r=tr;
			
		}else{
			t->r=tr->l;
			root=tr;
			root->l=t;
		}
		return cr;
	}
	if((cl-cr)==2){
		if(deep(tl->l)<deep(tl->r)){
			auto nroot=tl->r;
			t->l=nroot->r;
			tl->r=nroot->l;
			root=nroot;
			root->r=t;
			root->l=tl;
			
		}else{
			t->l=tl->r;
			root=tl;
			root->r=t;
		}
		return cl;
	}
	assert(0);
}

AVL树并不是非要旋转才行。